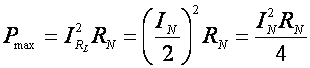Analisis de circuitos por teoremas

ANÁLISIS DE NODOS Y SUPERNODOS 

En análisis de circuitos eléctricos, el análisis de nodos, o método de tensiones nodales es un método para determinar la tensión (diferencia de potencial) de uno o más nodos.

Cuando se analiza un circuito por las leyes de Kirchhoff, se podrían usar análisis de nodos (tensiones nodales) por la ley de corrientes de Kirchhoff (LCK) o análisis de malla (corrientes de malla) usando la ley de tensiones de Kirchhoff (LVK). En el análisis de nodos se escribe una ecuación para cada nodo, con condición que la suma de esas corrientes sea igual a cero en cualquier instante, por lo que una carga ${\displaystyle \mathrm {Q} \,}$ nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por la conductancia. Por ejemplo, para un resistor, I_rama = V_rama * G, donde G es la Conductancia del resistor.

El análisis de nodos es posible cuando todos los nodos tienen conductancia. Este método produce un sistema de ecuaciones que puede resolverse a mano si es pequeño, o también puede resolverse rápidamente usando álgebra lineal en un computador. Por el hecho de que forme ecuaciones muy sencillas, este método es una base para muchos programas de simulación de circuitos (por ejemplo, SPICE). Cuando los elementos del circuito no tienen conductancia, se puede usar una extensión más general del análisis de nodos: el análisis de nodos modificado.

Los ejemplos simples de análisis de nodos se enfocan en elementos lineales. Las redes no lineales (que son más complejas) también se pueden resolver por el análisis de nodos al usar el método de Newton para convertir el problema no lineal en una secuencia de problemas lineales.

PASO 1: REFERENCIAR CADA ELEMENTO

Para facilitar la comprensión del circuito se referencia cada elemento del circuito, usando los subíndices S para las fuentes (sources)

PASO 2: ENUMERAR LOS NODOS Y ELEGIR UN NODO DE REFERENCIA

En un circuito con N nodos deberán haber N-1 voltajes desconocidos y N-1 ecuaciones. Se elige como nodo de referencia aquel al cual están conectadas el mayor número de ramas.

El nodo de referencia tiene cuatro ramas conectadas.

PASO 3: DEFINIR UN VOLTAJE ENTRE CADA NODO Y EL NODO DE REFERENCIA.

Supondremos que el nodo de referencia es de CERO VOLTIOS.

Debe haber N-1 voltajes de nodo desconocidos. Como hay tres nodos, hay 2 voltajes desconocidos, V1 y V2 y dos ecuaciones.

Los voltajes se definen entre pares de nodos. Se sobreentiende que el  voltaje colocado en cada uno de los nodos es el voltaje de ese nodo respecto al nodo de referencia. Si se elige un nodo de referencia diferente, los voltajes serán diferentes.

Esta es la única situación en la cual se usará el voltaje en el nodo sin los signos más-menos, exceptuando que se trate de una batería.

PASO 4: OBTNENER ECUACIONES. APLICAR LCK A CADA NODO

Para obtener un conjunto de ecuaciones se aplica LCK a cada nodo, excepto al de referencia, Al nodo de referencia nunca se aplica LCK.

Para evitar equivocaciones al aplicar LCK se recorre cada nodo en forma circular de izquierda a derecha, comenzando por la cola y terminando en la punta de flecha. Debe haber N-1 ecuaciones. Es decir, en este caso debe haber dos ecuaciones.

LCK en nodo N1

Se puede emplear suma de corrientes que entran igual  a cero, o suma de corrientes que salen igual a cero, o suma de corrientes que entran igual a suma de corrientes que salen. Se debe procurar no trazar las flechas de corriente en cada nodo, sino visualizarlas mentalmente. En este caso hemos considerado que todas las corrientes SALEN de cada nodo.

Aplicar la Ley de Ohm

Multiplicamos ambos lados por 10:

LCK en nodo N2

Multiplicamos ambos lados por 5:

Observe que:

Además, para la corriente I2, como V1 aparece primero la flecha va desde V1 hacia V2 , y para I4 la flecha va desde V2  hacia V1.

De nuevo, no es necesario colocar las fechas de corriente. Se ha hecho para dar claridad.

PASO 5: RESOLVER EL SISTEMA DE ECUACIONES

Se resuelve el sistema de ecuaciones, para obtener los voltajes de nodo, usando determinantes, o cualquier otro método de solución de ecuaciones como reducción, sustitución, igualación o eliminación gausiana.

Multiplicamos la Ec 2 por 7:

Sumamos Ec 1 y Ec 3:

Una vez obtenidos los voltajes es fácil obtener las corrientes aplicando la Ley de Ohm y LCK.

LINEALIDAD Y SUPERPOSICION

Elemento lineal

Elemento pasivo que tiene una relación lineal de voltaje contra corriente.

Es decir,

Si se multiplica por una constante K a la corriente (dependiente del tiempo) que fluye a través de un elemento, entonces el voltaje entre las terminales de ese elemento se verá a su vez multiplicado por la constante K.

Si v (t) se grafica como una función de i (t), el resultado es una línea recta.

Para un resistor:

Las ecuaciones que definen la relación V-I en el inductor y el capacitor también son lineales, al igual que la inductancia mutua.

Fuente dependiente lineal

Fuente dependiente (de corriente o de voltaje), cuya corriente o voltaje de salida son proporcionales solo a la primera potencia de alguna corriente o voltaje variable en el circuito, o a la suma de esas cantidades.

Circuito lineal

Aquel que se compone únicamente de:

• Fuentes independientes
• Fuentes dependientes lineales
• Elementos lineales (R, L, C)

Respuesta proporcional a la fuente

La multiplicación de todas las fuentes independientes de corriente y de voltaje por una constante K, aumenta todas las respuestas de corriente y voltaje por la  cantidad K, incluyendo a las salidas de las fuentes dependientes de voltaje o de corriente.

Ejemplo 1 respuesta proporcional a la fuente

Observe como al multiplicar la fuente Vs1 por K = 2, se aumenta la respuesta de corriente por la misma constante. Al pasar Vs1 de 10V a 20V, la respuesta de corriente pasa de 2A a 4A.

Ejemplo 2 respuesta proporcional a la fuente

Observe como al multiplicar la fuente Vs1 por K = 2, se aumentan las respuestas de corriente y voltaje por la misma constante.

Funciones de respuesta y excitación

Las fuentes fuerzan a las corrientes a circular por el circuito. Por eso reciben el nombre de funciones de excitación.

Los voltajes que producen se llaman funciones de respuesta o simplemente respuestas.

Tanto las funciones de excitación como las respuestas pueden ser funciones del tiempo.

El principio o teorema de superposición

Establece que la respuesta (una corriente o un voltaje) en cualquier parte de un circuito lineal que tenga más de una fuente independiente, se puede obtener como la suma de las respuestas individuales debidas a cada fuente independiente.

En otras palabras, en cualquier red resistiva lineal que contenga varias fuentes, el voltaje entre terminales o la corriente a través de cualquier resistor o fuente se puede calcular sumando algebraicamente todos los voltajes o corrientes individuales causados por cada fuente independiente, actuando individualmente. Es decir, todas las demás fuentes de voltaje independientes se sustituyen por cortocircuitos, y todas las fuentes de corriente independientes se sustituyen por circuitos abiertos. En cada momento solo hay activa una sola fuente independiente. Las fuentes dependientes permanecen siempre activas.

También pueden dejarse activas dos fuentes y desactivarse las demás. Se tratan entonces estas fuentes como una superfuente.

Una fuente también puede dividirse en varias fuentes. Sin embargo, el circuito más simple se obtiene cuando una fuente está completamente inactiva.

Ejemplo 1 principio de superposición

Ejemplo 2 principio de superposición

Generalmente, si un circuito tiene fuentes dependientes, el principio de superposición no ahorra tiempo.

Ejemplo 3 potencia y superposición.

La potencia no está sujeta a la superposición, pues es una respuesta no lineal  de grado 2.

Ahora, analizamos el circuito aplicando superposición con el fin de verificar si se obtienen los mismos resultados.

Vemos que, aunque la suma de potencias es cero, la suma de potencia de las fuentes no da -4W, y tampoco la potencia del resistor da 4W; por tanto,  la potencia no cumple el principio de superposición.

TRANSFORMACIÓN DE FUENTES

Se pueden intercambiar fuentes prácticas de voltaje o corriente sin afectar al resto del circuito.

Ejemplo 1 transformaciones de fuentes

1. Calcular IL en la fuente práctica de corriente
2. Transformar la fuente práctica de corriente en una fuente práctica de voltaje
3. Calcule IL si RL= 80 ohms en la fuente práctica de voltaje
4. Calcule la potencia suministrada por la fuente ideal en cada caso
5. ¿Qué valor de RL  absorberá la máxima potencia?
6. ¿Cuál es el valor de la potencia máxima?

Solución:

• Cálculo de IL : se usa un divisor de corriente.

• Transformación en una fuente práctica de voltaje

• Calcule IL si RL= 80 ohms en la fuente práctica de voltaje

• Cálculo de la potencia suministrada por la fuente ideal en cada caso.
• Potencia en la fuente de corriente.

• Potencia en la fuente de voltaje.

• ¿Qué valor de RL absorberá la máxima potencia?

• ¿Cuál es el valor de la potencia máxima?

Ejemplo 2 transformaciones de fuentes

1. Transformar ambas fuentes prácticas de voltaje de 24 V en fuentes prácticas de corriente.
2. Reducir resistores y fuentes ideales de corriente.
3. Transformar la fuente práctica de corriente resultante en una fuente práctica de voltaje.
4. Reducir fuentes ideales de voltaje.
5. Si Rx=2 ohms, busque la potencia entregada a Rx
6. Cuál es la máxima potencia que se puede entregar a cualquier valor de Rx?
7. Cuáles dos valores de Rx absorberán exactamente 5W?

Solución:

1. Transformar ambas fuentes prácticas de voltaje de 24 V en fuentes prácticas de corriente.

2. Reducir resistores y fuentes ideales de corriente. Los resistores R1 y R2 ohmios están en paralelo. Las fuentes de corriente se suman algebraicamente.

3. Transformar la fuente práctica de corriente resultante Is3 en una fuente práctica de voltaje.

4. Reducir fuentes ideales de voltaje.

5. Si Rx=2 ohms, busque la potencia entregada a Rx

6. Cuál es la máxima potencia que se puede entregar a cualquier valor de Rx ?
7. Cuáles dos valores de Rx  absorberán exactamente 5W?

TEOREMA DE SUPERPOSICIÓN

El teorema de superposición sólo se puede utilizar en el caso de circuitos eléctricos lineales, es decir circuitos formados únicamente por componentes lineales (en los cuales la amplitud de la corriente que los atraviesa es proporcional a la amplitud de voltaje a sus extremidades).

El teorema de superposición ayuda a encontrar:

• Valores de voltaje, en una posición de un circuito, que tiene más de una fuente independiente.
• Valores de corriente, en un circuito con más de una fuente independiente.

Este teorema establece que el efecto que dos o más fuentes tienen sobre una impedancia es igual, a la suma de cada uno de los efectos de cada fuente tomados por separado, sustituyendo todas las fuentes de voltaje restantes por un corto circuito, y todas las fuentes de corriente restantes por un circuito abierto.

Teorema de Thevenin

Cualquier red compuesta por resistores lineales, fuentes independientes y fuentes dependientes, puede ser sustituida en un par de nodos por un circuito equivalente formado por una sola fuente de voltaje y un resistor serie.

Por equivalente se entiende que su comportamiento ante cualquier red externa conectada a dicho par de nodos es el mismo al de la red original (igual comportamiento externo, aunque no interno).

La resistencia se calcula anulando las fuentes independientes del circuito (pero no las dependientes) y reduciendo el circuito resultante a su resistencia equivalente vista desde el par de nodos considerados. Anular las fuentes de voltaje equivale a cortocircuitarlas y anular las de corriente a sustituirlas por un circuito abierto.

El valor de la fuente de voltaje es el que aparece en el par de nodos en circuito abierto.

Teorema de Norton

Cualquier red compuesta por resistores lineales, fuentes independientes y fuentes dependientes puede ser sustituida, en un par de nodos, por un circuito equivalente formado por una sola fuentes de corriente y un resistor en paralelo.

La resistencia se calcula (igual que para el equivalente de Thevenin) anulando las fuentes independientes del circuito (pero no las dependientes) y reduciendo el circuito resultante a su resistencia equivalente vista desde el par de nodos considerados.

El valor de la fuente de corriente es igual a la corriente que circula en un cortocircuito que conecta los dos nodos.

 Equivalencia Thevenin-Norton

Se cumple:

4. Ejemplos

Dado el circuito:

1. Hallar el equivalente de Thevenin en bornas de la resistencia R (sin incluirla).

Queremos obtener un circuito de la forma:

Quitamos la resistencia R y vemos cual es el voltaje que hay entre los nodos a y b. El valor obtenido será el voltaje de Thevenin.

Se puede comprobar que la rama del resistor de 4 Ω no afecta.

Para hallar la resistencia de Thevenin anulamos las fuentes independientes y calculamos la resistencia vista desde los nodos a y b.

El circuito equivalente de Thevenin es:

2. Cálculo del equivalente Norton

Para calcular la corriente de Norton, cortocircuitamos:

Analizando aisladamente el circuito de dos mallas:

La resistencia es la misma que para el equivalente de Thevenin. El circuito equivalente es:

Como se puede observar, se cumple:

3. Ejemplo con fuentes dependientes

Calcular el equivalente de Thevenin del circuito:

Para calcular el voltaje de Thevenin se aplica movilidad:

Para el cálculo de la resistencia de Thevenin se anula el generador independiente, se conecta un generador de corriente (I) y se mide el voltaje (V):

TEOREMA DE MÁXIMA TRANSFERENCIA DE POTENCIA

Queremos determinar la potencia consumida por una resistencia en un circuito y cuál ha de ser el valor de dicha resistencia para que dicha potencia sea máxima.

Potencia disipada en R_L:

[1] 

¿Para qué valor de R_L será máxima la potencia?

Como R_N = R_TH, también R_L = R_N

La resistencia que disipa P_max entre dos terminales es la resistencia del circuito equivalente Thévenin o Norton.

¿Cuál es la potencia máxima transferida?

Debe elegirse: 

O también conocido el equivalente Norton:

Eligiendo R_L = R_N